Encrypting Data while Preserving Formatting with the Vault Enterprise Transform Secrets Engine

Vault 1.4 Enterprise introduced a new secrets engine called Transform. Transform is a secrets engine that allows Vault to encode and decode sensitive values residing in external systems such as databases or file systems. The Transform engine allows you to ensure that when a system is compromised, and its data is leaked, that the encoded secrets remain uncompromised even when held by an adversary. Unlike the Transit secrets engine, with Transform you can encrypt data while preserving the original formatting.

This post shows you how to implement Transform secrets into a simple API; source code is provided for both the Java and Go programming languages.

For information on the technical detail behind the Transform engine, please see Andy Manoske's blog post introducing this feature.

»Source code and example applications

To follow along with this post, a demo and all the example code can be found in the following repository.

https://github.com/nicholasjackson/demo-vault/tree/master/transform

To simply run the demo application, ensure Docker is running on your computer and run the following command in your terminal:

curl https://shipyard.run/apply | bash -s github.com/nicholasjackson/demo-vault/transform//blueprint

»Video demonstration

This blog post is also available as a recorded video on the HashiCorp YouTube channel:

»API Structure

The example application is a simple RESTful payment service that receives and stores payment data for later processing. The API has a single route that accepts an HTTP POST request, and it uses PostgreSQL for data storage.

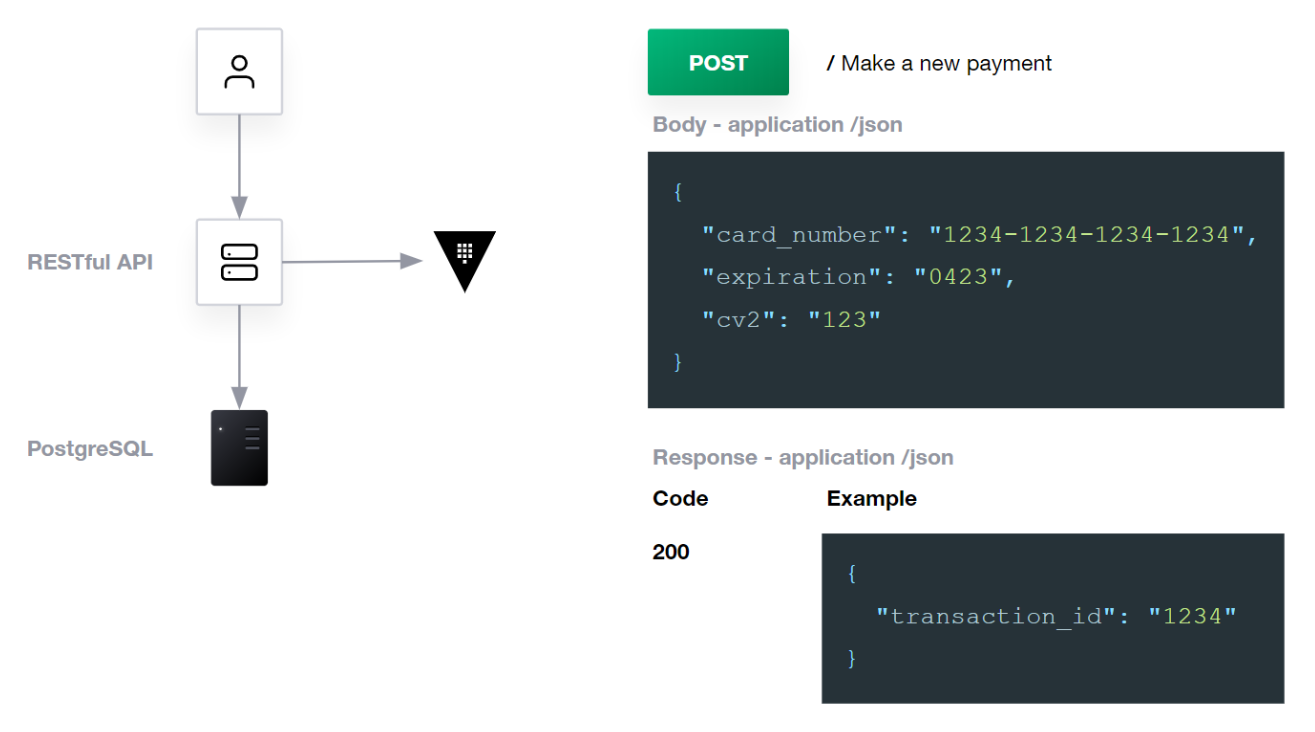
»Security Requirements

The security requirements for the API are:

• Credit card details must be stored in the database in an encrypted format at rest
• It must be possible to infer the bank and type of a card number without decrypting it

The first requirement is relatively trivial to solve using Vault and the Transit Secrets Engine. Transit secrets can be used as encryption as service to encrypt the credit card details before they are written to the database.

To satisfy the second requirement, you need to be able to query the type of the card and the bank which issued it. You can get this data from the card number as not all the data in a credit card number is unique. A credit card number is composed of three parts: the Issuer Number, the Account Number and the Checksum.

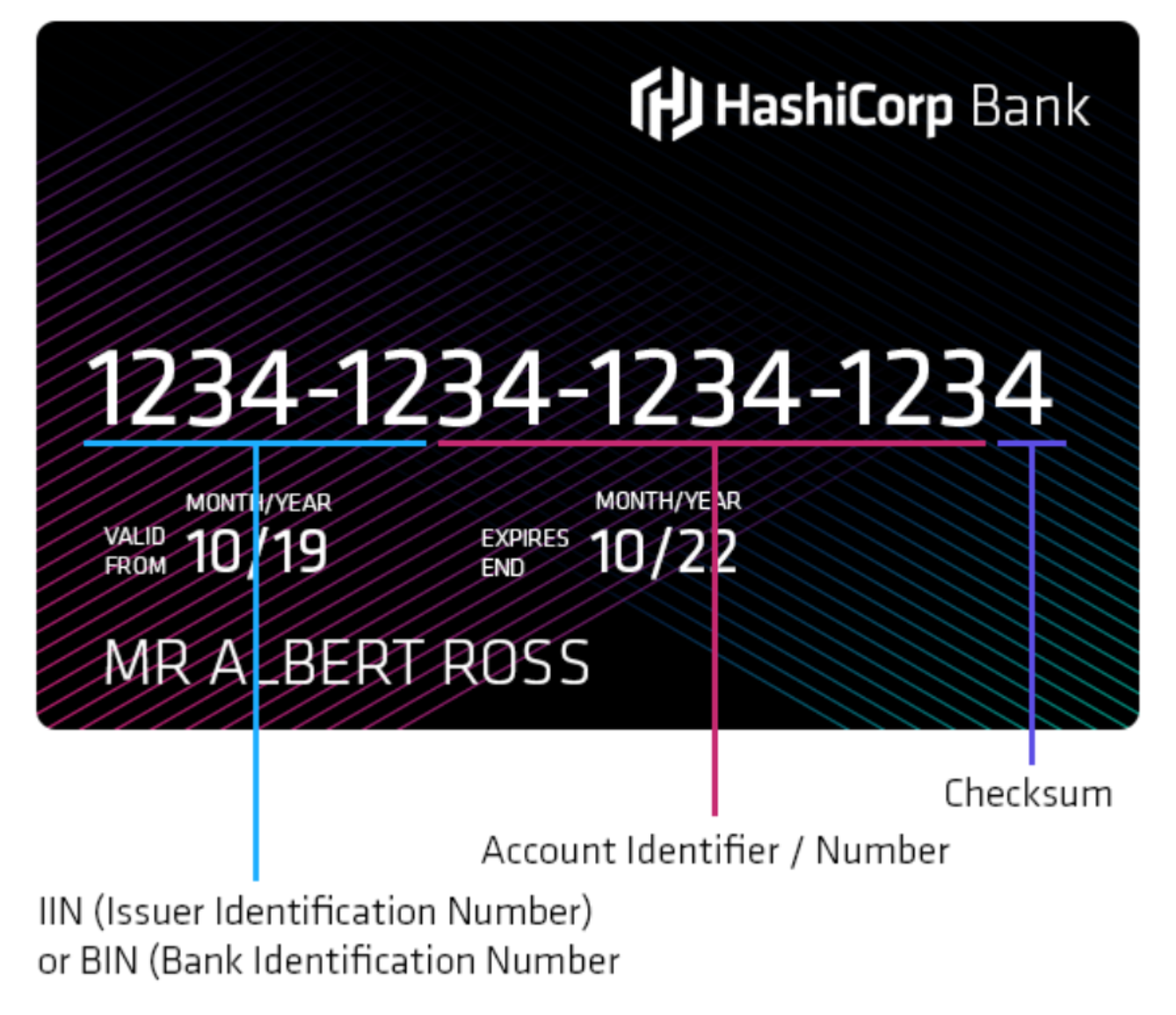
Issuer Number relates to the type of the card (first digit), and the issuer's code is the information that you would like to query to satisfy the second requirement.

Account Number is the unique identifier assigned to the holder of the card.

Checksum is not a secret part of the card number; instead, it is designed for quick error checking. The checksum is generated from the card number; before processing the checksum is regenerated using the Luhn algorithm, if the given and the computed checksums differ, then the card number has been entered incorrectly.

To be able to query the card issuer you realistically have two options:

1. Partially encrypt the card number in the database
2. Store metadata for the card along with the encrypted values

To implement this requirement in code, the developers have the responsibility for managing the complexity of partially encrypting the credit card data, and information security needs to worry about the correct implementation.

»Transform Secrets Engine

Vault's Transform Secrets Engine can be used to simplify the process while still satisfying the second requirement. Transform allows you to encrypt data while preserving formatting or to partially encrypt data based on a user-configurable formula. The benefits of this are that the info security team can centrally manage the definition for the encryption process, and the developers don’t need to worry about the implementation, they can use the Transform API to encrypt the card numbers.

In our use case where there is a need to partially encrypt the credit card numbers leaving the issuer as queryable data, a transform could be defined. This Transform takes a card number and encrypts the sensitive parts while retaining the formatting and ability to infer information about the card type and issuing bank.

Transforms are defined as regular expressions; the capture groups inside the expression are replaced with ciphertext, and anything outside the match groups is left in the original format.

To encrypt only the account number and checksum for a credit card number, you could use the following regular expression.

\d{4}-\d{2}(\d{2})-(\d{4})-(\d{4})

Given an input credit card number:

1234-5611-1111-1111

Vault would return ciphertext similar to the below example:

1234-5672-6649-0472

Note the first 6 digits have not been replaced with ciphertext as there are no capture groups in the regular expression for this text, the formatting of the data is also preserved as this was outside the capture groups.

»Real-world impact of partially encrypting data

You may be wondering, by only encrypting the account number and cv2 data, are you reducing the security of the encrypted card number?

The short answer is yes, but in real terms, it probably does not make a difference.

A number containing 16 digits has a possibility of 16^16 combinations, including the CV2 number. This roughly equates to 10 quintillion different permutations.

If you only store 10 digits of the card number plus the CV2, this is 10^13, or about 10 trillion combinations.

In reality, since the first 6 digits of a card number are the issuer and card type, there are not 1 million different issuers. Let's say there are 10,000, storing the full 16 digits would give you roughly 100 quadrillion combinations. In both cases, we need to remove the checksum, so we get 10 quadrillion combinations if you encrypt the account number and 1 trillion if you do not.

Yes, not encrypting the issuer means someone can make fewer guesses to determine the number, but they still need to make 1 trillion guesses. Assuming someone managed to obtain your database containing partially encrypted card numbers. If you had an average API request time of 100ms to accept or reject a payment, it would take about 190258 years for someone to brute force a payment. Even if the attacker was running parallel attacks, the odds are stacked heavily against them.

Fun math to one side, since we have determined it is secure to encrypt these credit card numbers partially, let's see how to do it.

»Configuring Transform Secrets

The Transform secrets engine is only available with Vault Enterprise version 1.4 and above. With all versions of Vault, only the Key/Value engine and the Cubbyhole secrets engines are enabled by default. To use the Transform secrets engine, it first needs to be enabled; you can do this using the following command.

vault secrets enable transform

After enabling the engine, several resources encapsulate different aspects of the transformation process that need to be configured before you can encrypt data. These are:

• Roles - Roles are the underlying high-level construct that holds the set of transformations that it is allowed to perform. The role name is provided when performing encode and decode operations.

• Transformations - Transformations hold information about a particular transformation. It contains information about the type of transformation that we want to perform, the template that it should use for value detection, and other transformation-specific values such as the tweak source or the masking character to use.

• Templates - Templates allow you to determine what and how to capture the value that you want to transform.

• Alphabets - Alphabets provide the set of valid UTF-8 characters in both the input and transformed value on FPE transformations.

Let's walk through each of the steps.

»Roles

First, we need to create a role called payments, when creating the role you provide the list of transformations that can be used from this role using the transformations parameter. The transformation ccn-fpe in the example role below does not yet exist. The transformations parameter is a "soft" constraint, while a role requires transforms to encode and decode data, they do not need to exist when creating the role.

vault write transform/role/payments transformations=ccn-fpe

»Transformations

Next, we create a transformation called ccn-fpe; this is the same name used when you created the role in the previous step. The parameter type defines the transform operation you would like to perform; this has two possible values:

• fpe - use Format Preserving Encryption using the FF3-1 algorithm
• masking - this process replaces the sensitive characters but is not reversible.

tweak_source is a non-confidential value stored alongside the ciphertext used when performing encryption and decryption operations. This parameter takes one of three permissible values, supplied, generated, internal. This example uses the internal value, which delegates the creation and storage of the tweak value to Vault. More information on tweak source can be found in the Vault documentation, https://www.vaultproject.io/docs/secrets/transform#tweak-source.

The template parameter relates to the template used by the Transform; you can define templates and reuse them across multiple transformations. Vault has two built-in Templates, which can be used builtin/creditcardnumber and builtin/socialsecuritynumber.

Finally, you specify the allowed_roles, specifying allowed roles ensures that the creator of the role is allowed to use this transformation.

vault write transform/transformation/ccn-fpe \
type=fpe \
tweak_source=internal \
template=ccn \
allowed_roles=payments

»Templates

The template defines what data is encrypted by the Transform. Templates are specified as regular expressions; the capture groups in the expression define the input elements, which is replaced with ciphertext.

The below example creates a template called ccn. The type parameter is set to regex which is currently the only option supported by the backend. Then you specify a pattern as a valid regular expression. For fpe transformations, you need to specify the alphabet, the alphabet is a custom character set used in the resulting ciphertext. alphabet can either be a custom alphabet like the example below or one of the built in values.

vault write transform/template/ccn \
type=regex \
pattern='\d{4}-\d{2}(\d{2})-(\d{4})-(\d{4})' \
alphabet=numerics

»Alphabets

Creating custom alphabets is an optional step for a transformation. Vault has several built-in alphabets covering common use-cases; however, you wish your ciphertext to be composed of a specific set of Unicode characters. To define a custom alphabet, you use the following command; this command creates a custom alphabet called numerics using the characters 0-9.

vault write transform/alphabet/numerics \
alphabet="0123456789"

»Testing the Transform

Now all of the components have been configured you can test the setup by writing data to the path transform/encode/payments, the part payments refers to the name of your Transform created in the previous steps.

vault write transform/encode/payments value=1111-2222-3333-4444

You will see an output that looks similar to the following. Note that the first 6 digits of the returned ciphertext are the same as the original data.

Key              Value
---              -----
encoded_value    1111-2200-1452-4879

To decode this ciphertext and reverse the operation, you write data to the transform/decode/payments path.

vault write transform/decode/payments value=<encoded_vaule>

vault write transform/decode/payments value=1111-2200-1452-4879

You will see output which looks similar to the below example:

Key              Value
---              -----
decoded_value    1111-2222-3333-4444

»Using Transform in your application

So far, you have seen how you can use the Transform engine using the CLI. To use the Transform engine from your application, you need to use Vault's API.

To interact with the Vault API, you have three options:

1. Use one of the Client libraries
2. Generate your own client from the OpenAPI v3 specifications
3. Manually interact with the HTTP API

This example follows the third option, as this demonstrates the simplicity of interacting with Vault's API.

»Using the Transform Encode API

The application only needs to encode data and not manage the configuration for Transform; to do this, it only needs to interact with a single API endpoint, which is Encode.

https://www.vaultproject.io/api-docs/secret/transform#encode

To encode data using transform secrets engine, you POST a JSON payload to the path /v1/transform/encode/:role_name, in this example :role_name is payments, which is the name of the role created earlier.

The API requires that you have a valid Vault token, and that token has the right policy allocated to it to operate. The Vault token is sent to the request using the X-Vault-Token HTTP header.

The payload for the request is a simple JSON structure with a single field value; you can see an example below.

{
  "value": "1111-2222-3333-4444"
}

If you were to use cURL to interact with the API and encode some data you could use the following command. You post the JSON payload to the path v1/transform/encode/payments along with the Vault token in an HTTP header.

curl localhost:8200/v1/transform/encode/payments \
  -H 'X-Vault-Token: root' \
  -d '{"value": "1111-2222-3333-4444"}'

The ciphertext for the submitted data is returned in the JSON response at .data.encoded_value. As you will see later on in the post it is a fairly trivial exercise to extract this information.

{
  "request_id": "0f170922-d7c1-0137-391b-932a2025beb4",
  "lease_id": "",
  "renewable": false,
  "lease_duration": 0,
  "data": {
    "encoded_value": "1111-2208-4340-0589"
  },
  "wrap_info": null,
  "warnings": null,
  "auth": null
}

Now, understanding the basics for interacting with the Vault API to encode data, let's see how this can be done from an application's code.

»Interacting with the Vault API from Java and Go

The first thing that needs to be done is to construct a byte array with a JSON formatted string for the payload. In both Go and Java common libraries easily handle this function.

»Go

// create the JSON request as a byte array
req := TokenRequest{Value: cc}
data, _ := json.Marshal(req)

»Java

// create the request
TokenRequest req = new TokenRequest(cardNumber);

// convert the POJO to a byte array 
ObjectMapper mapper = new ObjectMapper();
mapper.enable(SerializationFeature.INDENT_OUTPUT);
byte[] byteRequest = mapper.writeValueAsBytes(req);

Then a request can be constructed, the body of the request is set to the JSON data created in the previous step. You then make the request and retrieve the response from the server.

»Go

url := fmt.Sprintf("http://%s/v1/transform/encode/payments", c.uri)
r, _ := http.NewRequest(http.MethodPost, url, bytes.NewReader(data))
r.Header.Add("X-Vault-Token", "root")

resp, err := http.DefaultClient.Do(r)
if err != nil {
    return "", err
}
defer resp.Body.Close()

if resp.StatusCode != http.StatusOK {
    return "", fmt.Errorf("Vault returned response code %d, expected status code 200", resp.StatusCode)
}

»Java

// make a call to vault to process the request
URL url = new URL(this.url);
HttpURLConnection con = (HttpURLConnection)url.openConnection();
con.setDoOutput(true);    
con.setRequestMethod("POST");
con.setRequestProperty("Content-Type", "application/json; utf-8");
con.setRequestProperty("Accept", "application/json");
con.setRequestProperty("X-Vault-Token", this.token);

// write the body
try(OutputStream os = con.getOutputStream()) {
  os.write(byteRequest, 0, byteRequest.length);           
}

To read the JSON response from the Vault API, you can parse the body from the HTTP client into a simple structure.

»Go

// process the response
tr := &TokenResponse{}
err = json.NewDecoder(resp.Body).Decode(tr)
if err != nil {
    return "", err
}

»Java

// read the response
TokenResponse resp = new ObjectMapper()
  .readerFor(TokenResponse.class)
  .readValue(con.getInputStream());

The encoded data can now be passed to another function which will store it in the database.

Full source code for both examples can be found at https://github.com/nicholasjackson/demo-vault/tree/master/transform

»Testing the application

Let's test the application; the demo has both the Java and the Go code running, so you can use curl to test it.

curl localhost:9091 -H "content-type: application/json" -d '{"card_number": "1234-1234-1234-1234"}'

curl localhost:9092 -H "content-type: application/json" -d '{"card_number": "1234-1234-1234-1234"}'

You should see a response, something like the following.

{"transaction_id": 11}

To see the encrypted value for this transaction you can query the orders table on the database.

PGPASSWORD=password psql -h localhost -p 5432 -U root -d payments -c 'SELECT * from orders;'

This ciphertext can be validated using the CLI commands like in the previous example:

vault write transform/decode/payments value=<card_number>

»Summary

In this post, you have seen how the new Transform secrets engine can be used to partially encrypt credit card numbers at rest while preserving the formatting and ability to query the card issuer.

This example only covers one of the possibilities for the Transform secrets engine; if you have an interesting use case for Transform let us know, we would love to feature this in a future post.